提拉's Studio.

决策树分类

2025/02/16
loading

决策树基本定义

决策树是一种利用树形图进行决策的预测模型，表现出对象属性与对象值的一种映射关系，用于分类和回归任务。它是通过训练数据，采用自顶而下的贪婪算法选择最合适的属性作为节点生成的决策树。

属性选择标准

  1. 信息增益 （ID3算法）

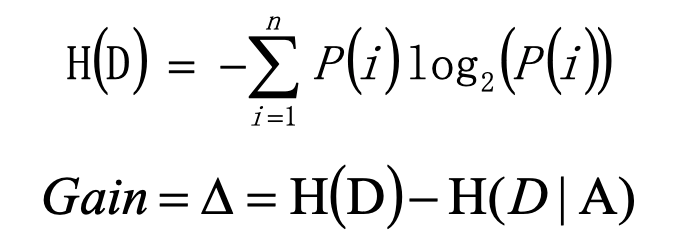
信息熵 H(D)用来描述系统信息量的不确定度，越混乱，信息熵越高。H(D|A)表示属性A的情况下的熵值。Gain值表示属性A对于系统统一性作出的贡献值，对比所有属性的Gain值，Gain值最高的属性适合做决策树的第一个节点。

条件熵：

eg. 风力weak的情况有8次，风力strong的情况6次。week情况下，8次中有6次出去玩，2次不出去玩。strong的情况下，6次中有3次出去玩，3次不出去玩。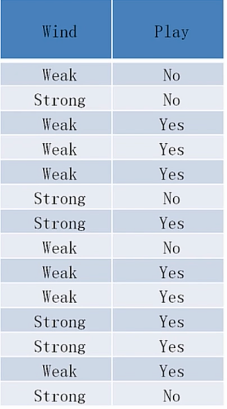

根据熵公式，
Entroy(weak) = -(0.25* $\log_2 0.25$) - （0.75* $\log_2 0.75$）= 0.8112781244591328
Entroy(strong) = -(0.5* $\log_2 0.5$) - （0.5* $\log_2 0.5$）= 1.0

1
2
3
4
5
6
p玩=1/4
p不玩=3/4
E玩=p玩*math.log(p玩,2)
E不玩=p不玩*math.log(p不玩, 2)
E某一属性=-E玩-E不玩
print(E某一属性)
  1. 信息增益比率 （C4.5算法）

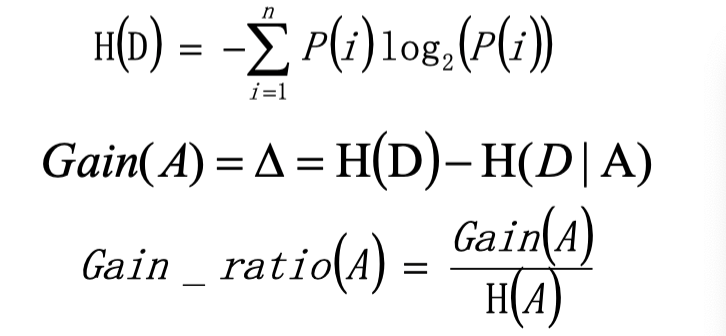
这种算法是ID3算法的进化，它排除了H(A)为0的情况，即如果有属性A发生的概率是1，就不使用这种属性作为决策树的节点。（如对象id这种属性，每一个值都是独特的，而它的对象映射的值也是确定的，因此概率是1。）

  1. 基尼系数/均方差 （CART算法 Classification and Regression Tree）

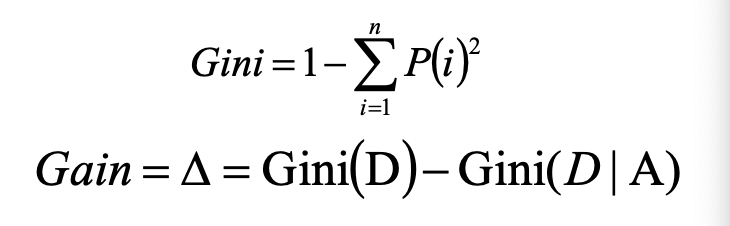
CART算法使用基尼系数（分类树）/均方差（回归树）作为属性节点的选择标准，选择GINI值最大的属性作为第一个节点，构建二叉树，越往下分，GINI值越小，代表分类效果越好。

分类树算法总结

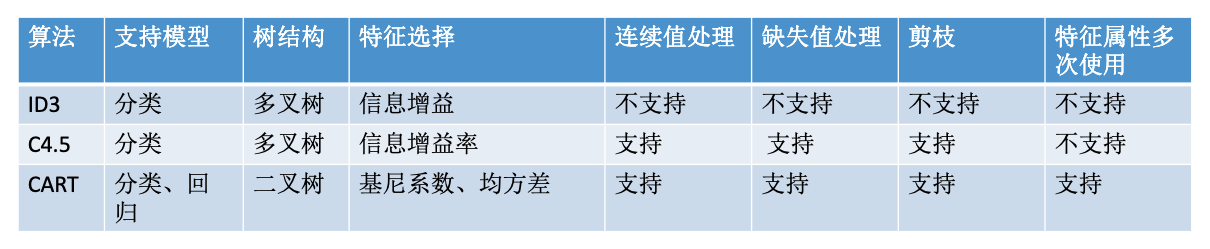
分类树 vs 回归树

分类树采用信息增益、信息增益比率、基尼系数来评价树的效果，是基于概率值判断的。分类树节点的预测值取当前分类属性下sample数最多的那个类别。

回归树中，节点的预测值一般为节点属性中所有值的均值。一般采用MSE作为树的评价指标，即均方差。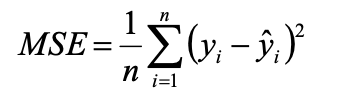

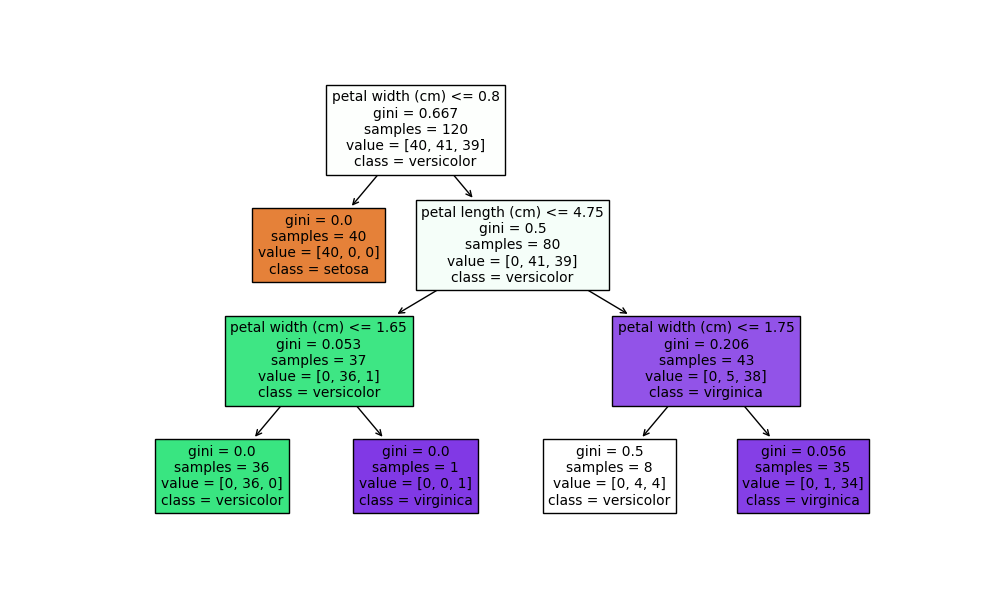
以sklearn中的iris数据集为训练集，使用决策树分类模型与回归模型，会直观得到以下：

决策树分类模型：

决策树回归模型：

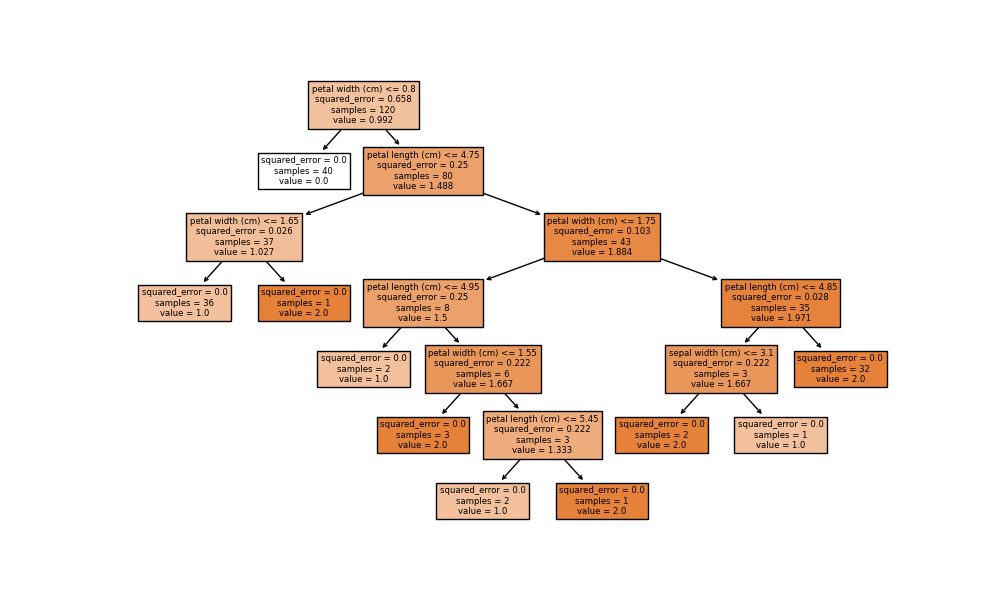
sklearn的iris数据集案例

共150组数据，其中120组为训练集，30组为测试集；每组数据有4个值，分别对应4个属性：sepal length，sepal width，petal length，petal width；3个类别：Setosa，Versicolour，Virginica。

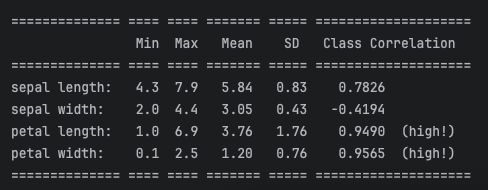
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

# 加载数据集
iris = datasets.load_iris()
X = iris['data']
y = iris.target

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建决策树分类器
clf = DecisionTreeClassifier(criterion='gini', max_depth=3)
clf2 = DecisionTreeRegressor()
# 训练模型

clf.fit(X_train, y_train)
clf2.fit(X_train, y_train)

# 预测测试集
y_pred = clf.predict(X_test)
y_pred2 = clf2.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"分类模型准确率: {accuracy}")

accuracy2 = accuracy_score(y_test, y_pred2)
print(f"回归模型准确率: {accuracy2}")

# 可视化决策树
plt.figure(figsize=(10, 6))
plot_tree(clf, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()


原文链接：https://tinaher.xyz/2025/02/16/%E5%86%B3%E7%AD%96%E6%A0%91%E5%88%86%E7%B1%BB/

发表日期：February 16th 2025, 10:39:08 am

版权声明：本文采用知识共享署名-非商业性使用 4.0 国际许可协议进行许可

CATALOG
  1. 1. 决策树基本定义
  2. 2. 属性选择标准
  3. 3. 分类树算法总结
  4. 4. 分类树 vs 回归树
  5. 5. sklearn的iris数据集案例
Total : 6
2025
2024