k-均值聚类
kmeans算法是一种常用的聚类算法,属于无监督学习的一种。
KMeans算法的基本原理是通过迭代的方式将数据集划分为K个簇,使得每个簇内的数据点尽可能相似,而不同簇之间的数据点尽可能不同。
具体步骤
初始化:随机选择K个数据点作为初始的聚类中心。
分配:计算每个数据点到各个聚类中心的距离,将每个数据点分配到距离最近的聚类中心所在的簇。
更新:重新计算每个簇的中心点,通常是取该簇所有数据点的均值。
迭代:重复步骤2和3,直到聚类中心不再发生变化或达到预设的迭代次数。
KMeans算法的应用场景和优缺点
KMeans算法因其简单高效,被广泛应用于数据挖掘、数据分析、异常检测、模式识别等领域。
优点:
简单高效:实现简单,收敛速度快。
应用广泛:适用于大规模数据集。
可解释性强:结果直观,易于理解。
缺点:
对初始值敏感:初始聚类中心的选择会影响最终结果。
可能陷入局部最优:算法容易陷入局部最优解而非全局最优解。
需要预先指定K值:K值的选取对结果有较大影响,通常需要根据经验或多次试验来确定。
KMeans算法的改进方法
K值选择:可以通过肘部法则、轮廓系数等方法来确定最佳的K值。
初始化方法:采用K-Means++算法来优化初始聚类中心的选择,避免随机选择带来的不稳定因素。
处理空簇:在迭代过程中检查并处理空簇,确保每个簇至少包含一个数据点。
代码实例
1 |
|
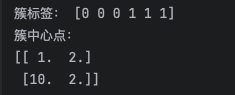
输出结果: