线性回归(Linear Regression)
线性回归是一种监督学习算法,用于建立连续型变量(因变量)与一个或多个自变量之间的线性关系模型。
核心思想:通过拟合最佳直线(或超平面)最小化预测值与真实值的误差。
数学模型

其中斜率系数代表权重参数。
损失函数
损失是一个数值指标,用于描述模型的预测有多大偏差。损失函数用于衡量模型预测与实际标签之间的距离。训练模型的目标是尽可能降低损失,将其降至最低值。
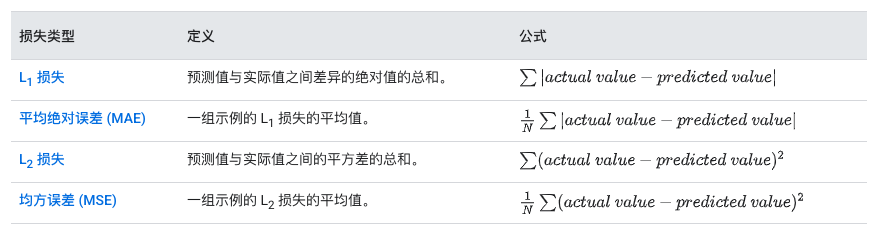
损失类型:
使用不同损失函数训练出的模型,与离群值距离不同。
MSE:模型更接近离群值,但与大多数其他数据点的距离更远。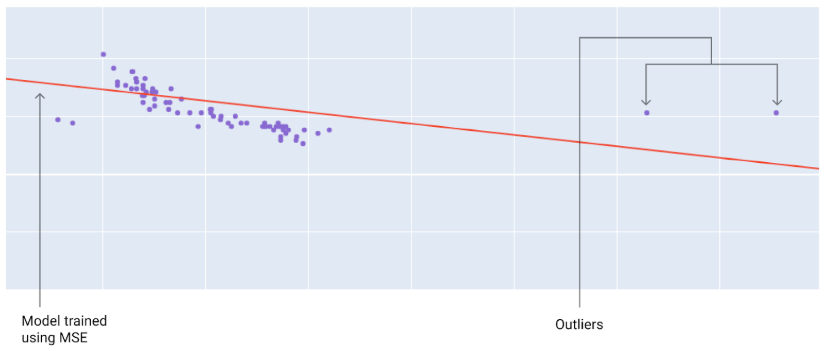
MAE:模型离离群值较远,但离大多数其他数据点较近。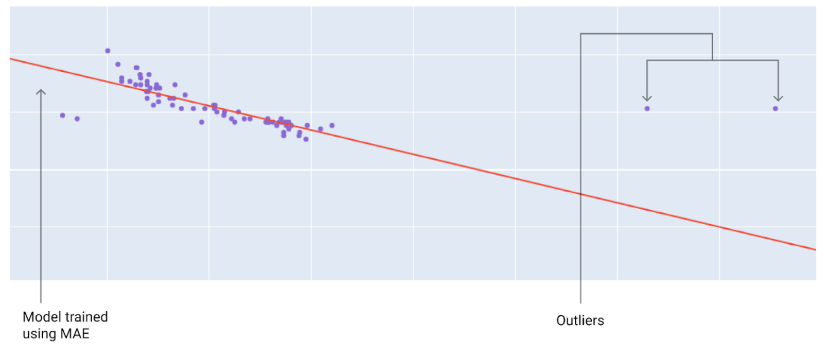
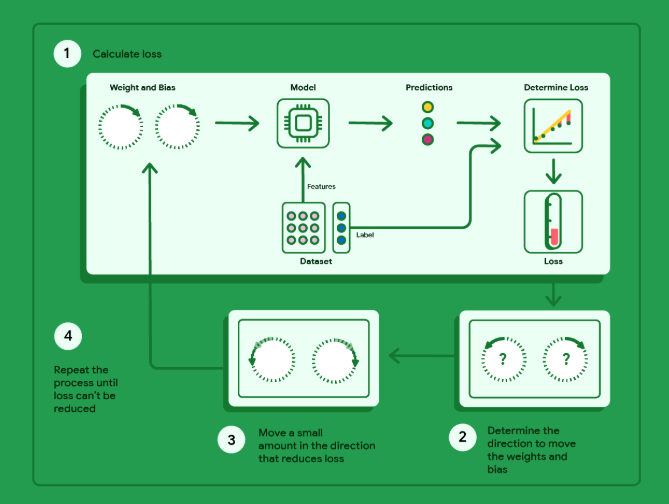
梯度下降法
梯度下降法是一种数学技术,能够以迭代方式找出权重和偏差,从而生成损失最低的模型。梯度下降法会针对用户指定的多次迭代重复以下过程,以找到最佳权重和偏差。
数学上来说主要是求f(x)函数的导数(含多阶导数)找到最佳权重与偏差,导数>0,则导数曲线为凹函数,存在最小值。
逻辑回归(Logistic Regression)
逻辑回归(Logistic Regression)是一种用于解决二分类问题的统计模型,通过S型函数将线性组合映射为0-1之间的概率值。虽名称含”回归”,实为分类算法。数学形态为sigmoid函数。
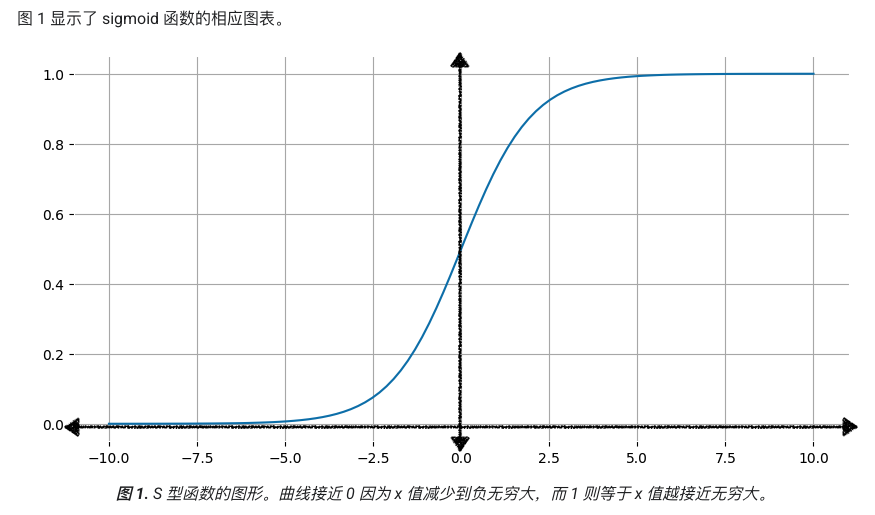
数学模型

损失函数
对数损失函数:

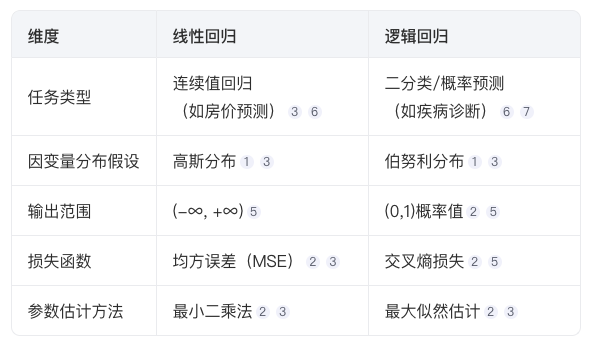
线性回归与逻辑回归异同点
核心关系
- 均属广义线性模型,通过线性组合建模特征与目标变量的关系。y=b+W1X1+ …+WnXn
- 逻辑回归在结构上可视为 “线性回归 + sigmoid激活函数”,将连续值映射为概率,相当于比线性回归多了一道工序。
本质区别