朴素贝叶斯分类
贝叶斯分类是一类分类算法的总称,这类算法以贝叶斯定理为基础。而朴素贝叶斯分类是贝叶斯分类中最简单与常见的一种分类方法,它与贝叶斯分类的区别点是加了一个前提假设:所有的条件对结果都是独立发生作用的,即所有的特征之间相互独立。
(比如某人是篮球运动员与某人有运动天赋,这两个特征之间是有关联的,不能算作完全独立。而特征有关联性会导致朴素贝叶斯概率误差较大)
贝叶斯公式
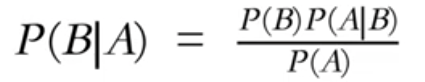
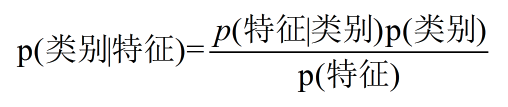
先验概率(Prior Probability):P(A)基于过去的经验认知,对某个事件发生概率的初步估计。
后验概率(Posterior Probability):P(A|B)表示在特征B已知的情况下,类别A发生的概率。后验概率是基于先验概率和新的证据,通过贝叶斯定理修正后的概率。
在实际情况中,我们利用贝叶斯算法去判断类别时,往往是基于多个特征,极大似然估计MLE是朴素贝叶斯分类模型的简化版,在计算出先验概率和条件概率之后,直接将两者对应乘积。下图中x表示特征,等式表示n个特征情况下是c类别的概率,即条件概率P(B|A)。

当特征数据离散时如何求概率:需要处理数据
1.数据离散化:等宽法,等频法,聚类法等。
2.假设数据服从正态分布,
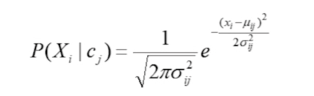
贝叶斯分类特点
- 属性可以离散,也可以连续。
- 数学基础坚实,分类效率稳定。
- 对缺失和噪声数据不太敏感。
- 属性如果不相关,分类效果很好。
贝叶斯项目使用
sklearn中有3种不同类型的朴素贝叶斯:
- 高斯分布型:假定属性/特征(连续数据)服从正态分布。
- 多项式型:属性/特征(离散值)。
- 伯努利型:属性/特征(只有0和1,即出现过和没出现过)。
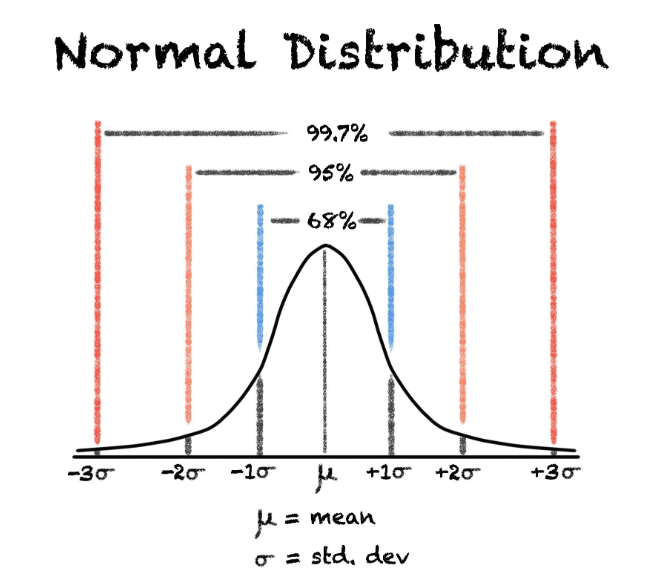
正态分布
正态分布也叫高斯分布,可以用来描述自然界和社会生活中的很多现象和事件,因为数据的分布往往都服从正态分布这个规律。它的形状由两个重要因素组成,正态分布的数学期望平均值μ和正态分布的标准差σ,标准差代表数据的离散程度,标准差越小,这组数就越集中。
贝叶斯思维
根据新的信息来不断更新迭代自己的认知,发现自己的偏差,从而作出更符合实际的判断。
4个重要组成部分:
1.先验概率:在一个事件未发生之前,根据先前的经验产生的主观猜测。
2.新的数据或信息:这使你决定是否更改先验概率使得一件事情的发生概率更符合新的情况。
3.后验概率:这由2,即上一条决定。
4.重复迭代。